The PVT block is the last one in the GNSS-SDR flow graph. Hence, it acts as a signal sink, since the stream of data flowing along the receiver ends here.

The role of a PVT block is to compute navigation solutions and deliver information in adequate formats for further processing or data representation.

It follows a description of the available positioning algorithms and their parameters, the available output formats, and the description of the configuration options for this block.

Positioning modes

The positioning problem is generally stated as

where \(\mathbf{y}\) is the measurement vector (that is, the observables obtained from the GNSS signals of a set of \(m\) satellites), \(\mathbf{x}\) is the state vector to be estimated (at least, the position of the receiver’s antenna and the time), \(\mathbf{h}(\cdot)\) is the function that relates states with measurements, and \(\mathbf{n}\) models measurement noise. Depending on the models, assumptions, available measurements, and the availability of a priori or externally-provided information, many positioning strategies and algorithms can be devised. It follows a description of the positioning modes available at the RTKLIB_PVT implementation, mostly extracted from the excellent RTKLIB manual.

Single Point Positioning

The default positioning mode is PVT.positioning_mode=Single. In this mode, the vector of unknown states is defined as:

where \(\mathbf{r}_r\) is the receiver’s antenna position in an earth-centered, earth-fixed (ECEF) coordinate system (in meters), \(c\) is the speed of light, and \(dt_r\) is the receiver clock bias (in seconds).

The measurement vector is defi

As described in the Observables block, for a signal from satellite \(s\) in the i-th band, the pseudorange measurement \(P_{r,i}^{(s)}\) can be expressed as:

In the current implementation, if the receiver obtains pseudorange measurements from the same satellite in different frequency bands, only measurements in the L1 band are used.

Hence, the equation that relates pseudorange measurements to the vector of unknown states can be written as:

The geometric range \(\rho_r^{(s)}\) is defined as the physical distance between the satellite antenna phase center position and the receiver antenna phase center position in the inertial coordinates. For the expression in the ECEF coordinates, the earth rotation effect has to be incorporated. This is known as the Sagnac effect¹, and it can be approximated by:

\(\begin{equation} \rho_{r}^{(s)} \approx \left\| \mathbf{r}_r(t_r) - \mathbf{r}^{(s)}(t^{(s)}) \right\| + {\definecolor{dark-orange}{RGB}{255,165,0} \color{dark-orange} \frac{\omega_e}{c}\left(x^{(s)}y_r - y^{(s)}x_r \right)}~, \end{equation}\) where \(\omega_e\) is the Earth rotation angle velocity (in rad/s).

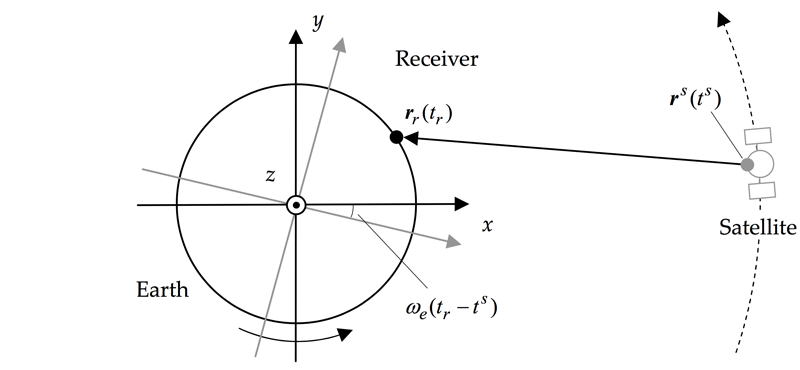Geometric range and Earth rotation correction ²

Equation \(\mathbf{h}(\mathbf{x})\) is clearly nonlinear due to the presence of the Euclidean norm operator \(\left\| \cdot \right\|\). However, this term can be extended by using Taylor series around an initial parameter vector \(\mathbf{x}_0\) as \(\mathbf{h}(\mathbf{x}) = \mathbf{h}(\mathbf{x}_0) + \mathbf{H}(\mathbf{x}-\mathbf{x}_0) + ...\), where \(\mathbf{H} = \frac{\partial \mathbf{h}(\mathbf{x})}{\partial \mathbf{x}} \bigg\rvert_{\mathbf{x} = \mathbf{x}_{0} }\) is a partial derivatives matrix of \(\mathbf{h}(\mathbf{x})\) with respect to \(\mathbf{x}\) at \(\mathbf{x} = \mathbf{x}_{0}\). Assuming that the initial parameters are adequately near the true values and the second and further terms of the Taylor series can be neglected, equation \(\mathbf{y} = \mathbf{h}(\mathbf{x}) + \mathbf{n}\) can be approximated by \(\mathbf{y} \approx \mathbf{h}(\mathbf{x}_0) + \mathbf{H}(\mathbf{x}-\mathbf{x}_0) + \mathbf{n}\), and then we can obtain the following linear equation:

which can be solved by a standard iterative weighted least squares method.

Matrix \(\mathbf{H}\) can be written as:

and the weighted least squares estimator (LSE) of the unknown state vector is obtained as:

For the initial parameter vector \(\mathbf{x}_0\) for the iterated weighted LSE, just all \(0\) are used for the first epoch of the single point positioning. Once a solution obtained, the position is used for the next epoch initial receiver position. For the weight matrix \(\mathbf{W}\), the RTKLIB_PVT implementation uses:

where:

• \(F^{(s)}\) is the satellite system error factor. This parameter is set to \(F^{(s)} = 1\) for GPS and Galileo.

• \(R_r\) is the code/carrier‐phase error ratio. This value is set by default to \(R_r = 100\), and can be configured with the PVT.code_phase_error_ratio_l1 option.

• \(a_{\sigma}, b_{\sigma}\) is the carrier‐phase error factor \(a\) and \(b\) (in m). They are set by default to \(a_{\sigma} = b_{\sigma} = 0.003\) m, and can be configured with the PVT.carrier_phase_error_factor_a and PVT.carrier_phase_error_factor_b options, respectively.

• \(El_r^{(s)}\) is the elevation angle of satellite direction (in rad).

• \(\sigma_{bclock,s}\) is the standard deviation of the broadcast ephemeris and clock error (in m). This parameter is estimated internally from URA (User Range Accuracy) or or similar indicators.

• \(\sigma_{ion,s}\) is the standard deviation of ionosphere correction model error (in m). This parameter is set to \(\sigma_{ion} = 5\) m by default (PVT.iono_model=OFF) and \(\sigma_{ion} = 0.5 \cdot I_{r,i}^{(s)}\) m when the option PVT.iono_model=Broadcast is set in the configuration file.

• \(\sigma_{trop,s}\) is the standard deviation of troposphere correction model error (in m). This parameter is set to \(\sigma_{trop} = 3\) m by default (PVT.trop_model=OFF) and \(\sigma_{trop} = 0.3 / \left(\sin(El_r^{(s)}) + 0.1\right)\) m when the option PVT.trop_model=Saastamoinen, PVT.trop_model=Estimate_ZTD or PVT.trop_model=Estimate_ZTD_Grad is set in the configuration file.

• \(\sigma_{cbias}\) is the standard deviation of code bias error (in m). This parameter is set to \(\sigma_{cbias} = 0.3\) m.

In addition, two optional terms can extend this error model. These options are only present in the next branch of the upstream repository, and will be included in the next GNSS-SDR stable release.

• An SNR-dependent term, activated when PVT.error_factor_snr is set to a positive value \(e_{\sigma}\) (in m; ta recommended value is \(0.005\) m), which adds to the variance a term

  \[e_{\sigma}^2 \cdot 10^{~0.1 \cdot \max \left( \text{SNR}_{\text{max}} - C/N_0^{(s)},~ 0 \right)}~,\]

  where \(C/N_0^{(s)}\) is the carrier-to-noise density ratio reported by the tracking loop for satellite \(s\), and \(\text{SNR}_{\text{max}}\) is a reference value (in dB-Hz) above which no penalty is applied, configurable with PVT.error_snr_max (it defaults to \(52\) dB-Hz). It defaults to \(0.0\) (disabled), preserving the elevation-only error model.

• A receiver-reported standard deviation term, activated when PVT.error_factor_rcv_std is set to a positive value, which weights each observation with the pseudorange / carrier-phase standard deviations reported in the observation structure (fields ready to be populated from the tracking-loop variance estimates). It defaults to \(0.0\) (disabled).

By default, the receiver clock bias estimated in single point positioning is assumed to be common to all GPS-like signals, including QZSS. Setting PVT.estimate_qzss_isb=true adds a separate QZS-GPS inter-system bias to the vector of unknowns. The estimated offset is reported in the RTKLIB solution structure (sol.dtr[4]). Since the extra unknown requires one more satellite in mixed GPS + QZSS epochs, which degrades availability under limited sky visibility, this option defaults to false and should only be enabled in open-sky scenarios with six or more satellites in view. This option is only present in the next branch of the upstream repository, and will be included in the next GNSS-SDR stable release.

The estimated receiver clock bias \(dt_r\) is not explicitly output, but incorporated in the solution time‐tag. That means the solution time‐tag indicates not the receiver time‐tag but the true signal reception time measured in GPS Time.

Solution validation

The estimated receiver positions described in (\(\ref{eq:lse}\)) might include invalid solutions due to unmodeled measurement errors. To test whether the solution is valid or not, and to reject the invalid solutions, the RTKLIB_PVT applies the following validation tests after obtaining the receiver’s position estimate:

1) Residuals Test

Defining the residuals vector \(\boldsymbol{\nu} = \left( \nu_1, \nu_2, \nu_3, ..., \nu_m \right)^T\) with:

the residuals test is defined as:

where \(n\) is the number of estimated parameters, \(m\) is the number of measurements, \(\chi_{\alpha}^2(n)\) is the chi‐square distribution of degree of freedom \(n\), and with a significance level of \(\alpha=0.001\) (that is, \(prob > 0.001\)).

2) GDOP Test

The Geometric Dilution of Precision, defined as \(\text{GDOP} = \sqrt{\sigma_{r_{x}}^2 + \sigma_{r_{y}}^2 + \sigma_{r_{z}}^2 + \sigma_{c \cdot dt}^2 }\), must be better (that is, lower) than a certain threshold:

The threshold value is set by default to \(\text{GDOP}_{\text{threshold}} = 30\), and it can be configured via the option PVT.threshold_reject_GDOP in the configuration file.

If any of the validation fails, the solution is rejected as an outlier (that is, no solution is provided).

Receiver Autonomous Integrity Monitoring (RAIM)

In addition to the solution validation described above, RAIM (receiver autonomous integrity monitoring) FDE (fault detection and exclusion) function can be activated. If the chi-squared test described above fails and the option PVT.raim_fde is set to \(1\), the implementation retries the estimation by excluding one by one of the visible satellites. After all of the retries, the estimated receiver position with the minimum normalized squared residuals \(\boldsymbol{\nu}^T \boldsymbol{\nu}\) is selected as the final solution. In such a scheme, an invalid measurement, which might be due to satellite malfunction, receiver fault, or large multipath, is excluded as an outlier. Note that this feature is not effective with two or more invalid measurements. It also needs two redundant visible satellites, which means at least 6 visible satellites are necessary to obtain the final solution.

Precise Point Positioning

When the PVT.positioning_mode option is set to PPP_Static or PPP_Kinematic in the configuration file, a Precise Point Positioning algorithm is used to solve the positioning problem. In this positioning mode, the state vector to be estimated is defined as:

where \(Z_r\) is ZTD (zenith total delay), \(G_{N_r}\) and \(G_{E_r}\) are the north and east components of tropospheric gradients (see the tropospheric model below) and \(\mathbf{B}_{LC} = \left( B_{r,LC}^{(1)}, B_{r,LC}^{(2)}, B_{r,LC}^{(3)}, ..., B_{r,LC}^{(m)} \right)^T\) is the ionosphere‐free linear combination of zero‐differenced carrier‐phase biases (in m), defined below in Equation (\(\ref{eq:bias-lc}\)).

The Precise Point Positioning measurement model is based on the fact that, according to the phase and code ionospheric refraction, the first order ionospheric effects on code and carrier-phase measurements depend (99.9 %) on the inverse of squared signal frequency \(f_i\). Thence, dual-frequency receivers can eliminate their effect through a linear combination of pseudorange \(P_{r,i}^{(s)}\) and phase-range \(\Phi_{r,i}^{(s)}\) measurements (where the definitions at Observables apply):

with \(C_i = \frac{f_i^2}{f_i^2 - f_j^2}\) and \(C_j = \frac{-f_j^2}{f_i^2 - f_j^2}\), where \(f_i\) and \(f_j\) are the frequencies (in Hz) of \(L_i\) and \(L_j\) measurements. Explicitly:

with

In the current implementation, satellites and receiver antennas offset and variation are not applied, so \(\mathbf{d}_{r,pco,i} = \mathbf{d}_{pco,i}^{(s)} = \mathbf{0}\) and \(d_{r,pcv,i} = d_{pcv,j}^{(s)} = 0\). The correction terms for the Earth tide³ \(\mathbf{d}_{r,disp}\) and the phase windup effect⁴ \(\phi_{pw}\) are deactivated by default, and can be activated through the PVT.earth_tide and PVT.phwindup options, respectively.

The measurement vector is then defined as:

where \(\boldsymbol{\Phi}_{LC} = \left(\Phi_{r,LC}^{(1)}, \Phi_{r,LC}^{(2)}, \Phi_{r,LC}^{(3)}, ..., \Phi_{r,LC}^{(m)} \right)^T\) and \(\mathbf{P}_{LC} = \left( P_{r,LC}^{(1)}, P_{r,LC}^{(2)}, P_{r,LC}^{(3)}, ..., P_{r,LC}^{(m)} \right)^T\).

In the current implementation, if the receiver obtains pseudorange measurements from the same satellite in different frequency bands, only measurements in the L1 band are used.

The equation \(\mathbf{h}(\mathbf{x})\) that relates measurements and states is:

where:

This is again a nonlinear equation that could be solved with the iterative weighted least squares estimator as in the case of the Single Point Positioning case. However, here we want to incorporate some a priori information, such as a basic dynamic model for the receiver, and some statistical knowledge about the status of the troposphere. The Extended Kalman Filter offers a suitable framework for that.

The partial derivatives matrix \(\mathbf{H} = \frac{\partial \mathbf{h}(\mathbf{x})}{\partial \mathbf{x}} \bigg\rvert_{\mathbf{x} = \mathbf{x}_{0} }\) can be written as:

where \(\mathbf{D} = \left( \begin{array}{ccccc} 1 & -1 & 0 & \cdots & 0 \\ 1 & 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & \cdots & -1 \end{array} \right)\) is known as the single‐differencing matrix, \(\mathbf{E} = \left( \mathbf{e}_{r}^{(1)}, \mathbf{e}_{r}^{(2)}, \mathbf{e}_{r}^{(3)}, ..., \mathbf{e}_{r}^{(m)} \right)^T\) with \(\mathbf{e}_{r}^{(s)}\) defined as in equation (\(\ref{eq:H-single}\)), and

\(\scriptstyle \begin{equation} \!\!\!\!\!\!\!\!\!\!\! \mathbf{M}_T \; = \; \left( \begin{array}{ccc} m_{WG,r}^{(1)} \left( El_r^{(1)} \right) & m_{W,r}^{(1)} \left( El_r^{(1)} \right) \cot \left( El_r^{(1)} \right) \cos \left( Az_r^{(1)} \right) & m_{W,r}^{(1)} \left( El_r^{(1)} \right) \cot \left( El_r^{(1)} \right) \sin \left( Az_r^{(1)} \right) \\ m_{WG,r}^{(2)} \left( El_r^{(2)} \right) & m_{W,r}^{(2)} \left( El_r^{(2)} \right) \cot \left( El_r^{(2)} \right) \cos \left( Az_r^{(2)} \right) & m_{W,r}^{(2)} \left( El_r^{(2)} \right) \cot \left( El_r^{(2)} \right) \sin \left( Az_r^{(2)} \right) \\ m_{WG,r}^{(3)} \left( El_r^{(3)} \right) & m_{W,r}^{(3)} \left( El_r^{(3)} \right) \cot \left( El_r^{(3)} \right) \cos \left( Az_r^{(3)} \right) & m_{W,r}^{(3)} \left( El_r^{(3)} \right) \cot \left( El_r^{(3)} \right) \sin \left( Az_r^{(3)} \right) \\ \vdots \\ m_{WG,r}^{(m)} \left( El_r^{(m)} \right) & m_{W,r}^{(m)} \left( El_r^{(m)} \right) \cot \left( El_r^{(m)} \right) \cos \left( Az_r^{(m)} \right) & m_{W,r}^{(m)} \left( El_r^{(m)} \right) \cot \left( El_r^{(m)} \right) \sin \left( Az_r^{(m)} \right) \end{array} \right) \end{equation}\) is a matrix related to the tropospheric model (see below).

With all those definitions, the Precise Point Positioning solution is computed as follows:

The transition matrix \(\mathbf{F}_k\) models the receiver movement:

• If PVT.positioning_mode=PPP_Static:

• If PVT.positioning_mode=PPP_Kinematic:

where \(\Delta_k = t_{k+1} - t_k\) is the time between GNSS measurements, in s.

The dynamics model noise covariance matrix \(\mathbf{Q}_k\) is set to:

with:

• \(\mathbf{Q}_r = \mathbf{E}_r^T \text{diag} \left( \sigma_{re}^2 , \sigma_{rn}^2 , \sigma_{ru}^2 \right) \mathbf{E}_r\), where \(\mathbf{E}_r\) is the coordinates rotation matrix from ECEF to local coordinates at the receiver antenna position (defined below), and \(\sigma_{re}\), \(\sigma_{rn}\) and \(\sigma_{ru}\) are the standard deviations of east, north, and up components of the receiver position model noises (in m).
  • If the positioning mode is set to PVT.positioning_mode=PPP_Static, these values are initialized to \(\sigma_{re} = \sigma_{rn} = \sigma_{ru} = 100\) m in the first epoch and then set to \(0\) in the following time updates.
  • If the positioning mode is set to PVT.positioning_mode=PPP_Kinematic, these values are set to \(\sigma_{re} = \sigma_{rn} = \sigma_{ru} = 100\) m for all time updates.
• \(\mathbf{Q}_v = \mathbf{E}_r^T \text{diag} \left( \sigma_{ve}^2 \Delta_k , \sigma_{vn}^2 \Delta_k, \sigma_{vu}^2 \Delta_k \right) \mathbf{E}_r\), where \(\sigma_{ve}\), \(\sigma_{vn}\) and \(\sigma_{vu}\) are the standard deviations of east, north, and up components of the receiver velocity model noises (in m/s/\(\sqrt{s}\)). In the current implementation, those parameters are set to \(\sigma_{ve} = \sigma_{vn} = \sigma_{vu} = 0\).
• \(\sigma_{c \cdot dt_{r}}\) is the standard deviation of the receiver clock offset (in m). This value is set to \(\sigma_{c \cdot dt_{r}} = 100\) m.
• \(\mathbf{Q}_{T} = \text{diag} \left( \sigma_{Z}^2 \Delta_k, \sigma_{G_{N}}^2 \Delta_k, \sigma_{G_{E}}^2 \Delta_k \right)\) is the noise covariance matrix of the troposphere terms. These values are set to \(\sigma_{Z} = 0.0001\), and \(\sigma_{G_{N}} = \sigma_{G_{E}}\) are initialized to \(\sigma_{G_{N}} = \sigma_{G_{E}} = 0.001\) m/\(\sqrt{s}\) in the first epoch and then set to \(\sigma_{G_{N}} = \sigma_{G_{E}} = 0.1 \cdot \sigma_{Z}\) in the following time updates. The default value of \(\sigma_{Z} = 0.0001\) m/\(\sqrt{s}\) can be configured with the PVT.sigma_trop option.
• \(\sigma_{bias}\) is the standard deviation of the ionosphere-free carrier-phase bias measurements, in m/\(\sqrt{s}\). This value is initialized at the first epoch and after a cycle slip to \(\sigma_{bias} = 100\) m/\(\sqrt{s}\), and then is set to a default value of \(\sigma_{bias} = 0.0001\) m/\(\sqrt{s}\) in the following time updates. This value and can be configured with the option PVT.sigma_bias.
• \(\mathbf{E}_r = \left( \begin{array}{ccc} - \sin(\theta_r) & \cos (\theta_r) & 0 \\ -\sin (\psi_r) \cos(\theta_r) & - \sin (\psi_r)\sin(\theta_r) & \cos (\psi_r) \\ \cos(\psi_r)\cos(\theta_r) & \cos(\psi_r)\sin(\theta_r) & \sin(\psi_r)\end{array} \right)\) is the rotation matrix of the ECEF coordinates to the local coordinates, where \(\psi_r\) and \(\theta_r\) are the geodetic latitude and the longitude of the receiver position.

The measurement model noise covariance matrix \(\mathbf{R}_k\) is defined as:

where:

in which \(\sigma_{\Phi,1}^{(s)}\) is the standard deviation of L1 phase‐range measurement error (in m), and \(\sigma_{P,1}^{(s)}\) is the standard deviation of L1 pseudorange measurement error (in m). These quantities are estimated as:

• \({\sigma_{\Phi,1}^{(s)}}^2 = a_{\sigma}^2 + \frac{b_{\sigma}^2}{\sin(E_r^{(s)})^2} + \sigma_{ion,s}^2 + \sigma_{bclock}^2 + \sigma_{trop,s}^2\), where:
  • \(a_{\sigma} = 0.003\) and \(b_{\sigma} = 0.003\) are the carrier phase error factors (configurable via PVT.carrier_phase_error_factor_a and PVT.carrier_phase_error_factor_b),
  • \(\sigma_{ion,s}\) is the standard deviation of ionosphere correction model error (in m). This parameter is set to \(\sigma_{ion} = 5\) m by default (PVT.iono_model=OFF) and \(\sigma_{ion} = 0.5 \cdot I_{r,i}^{(s)}\) m when the option PVT.iono_model=Broadcast is set in the configuration file.
  • \(\sigma_{bclock} = 30\) m is the standard deviation of the broadcast clock,
  • \(\sigma_{trop}\) is the standard deviation of the troposphere correction model error (in m). This parameter is set to \(\sigma_{trop} = 3\) m when PVT.trop_model=OFF and \(\sigma_{trop,s} = \frac{0.3}{\sin(El_r^{(s)}) + 0.1}\) m when PVT.trop_model=Saastamoinen, PVT.trop_model=Estimate_ZTD or PVT.trop_model=Estimate_ZTD_Grad.
• \({\sigma_{P,1}^{(s)}}^2 = R_r \cdot \left( a_{\sigma}^2 + \frac{b_{\sigma}^2}{\sin(E_r^{(s)})^2} \right) + \sigma_{ion,s}^2 + \sigma_{bclock}^2 + \sigma_{trop,s}^2 + \sigma_{cbias}^2\), where:
  • \(R_r = 100\) (configurable via PVT.code_phase_error_ratio_l1),
  • \(a_{\sigma} = b_{\sigma} = 0.003\) m (configurable via PVT.carrier_phase_error_factor_a and PVT.carrier_phase_error_factor_b),
  • \(\sigma_{ion,s}\), \(\sigma_{bclock}\) and \(\sigma_{trop,s}\) defined as above.
  • \(\sigma_{cbias}\) is the standard deviation of code bias error (in m). This parameter is set to \(\sigma_{cbias} = 0.3\) m.

Outlier rejection

In each of the executions of the Extended Kalman Filter defined in (\(\ref{eq:state-update}\))-(\(\ref{eq:meas-cov-update}\)), if the absolute value of a residual \(\nu_s = \frac{P_r^{(s)} - \left( \hat{\rho}_r^{(s)} +c \hat{dt}_r - c \cdot dT^{(s)} + I_r^{(s)} + T_r^{(s)} \right)}{\sigma_s}\) for a satellite \(s\) is above a certain threshold, that observation is rejected as an outlier. The default threshold is set to \(30\) m and can be configured via the option PVT.threshold_reject_innovation.

The rejection threshold can be set separately for code and carrier-phase observables: PVT.threshold_reject_innovation applies to code observables, and a new PVT.threshold_reject_innovation_phase option applies to carrier-phase observables. The latter defaults to the value of the former, so existing configurations behave identically; a value of \(5.0\) m for the phase threshold in RTK modes. The separate phase threshold is only present in the next branch of the upstream repository, and will be included in the next GNSS-SDR stable release.

Real-Time Kinematic

Warning: The Real-Time Kinematic positioning modes and the NTRIP client described in this section are only available from the next branch of the upstream GNSS-SDR repository. They will be included in the next stable release.

When the PVT.positioning_mode option is set to Static or Kinematic in the configuration file, the positioning problem is solved by relative positioning with respect to a base station of known coordinates, using double-differenced carrier-phase and pseudorange measurements. Static assumes a stationary rover antenna, while Kinematic models a moving receiver. In this operation mode, commonly known as Real-Time Kinematic (RTK), most of the common error sources (satellite orbit and clock errors, and, for short baselines, ionospheric and tropospheric delays) cancel out in the differencing, and centimeter-level accuracy becomes achievable once the carrier-phase integer ambiguities are resolved.

The current implementation supports a fixed (that is, static) base station broadcasting its position and its observations over the RTCM 3 protocol, received through the NTRIP client described below. Per constellation, and freely combined, the receiver may run GPS L1 C/A alone or together with one of L2C or L5, Galileo E1 alone or together with E5a, and BeiDou B1C (single-frequency). Single-band sets run single-frequency RTK, which is viable on the short effective baselines of VRS services and benefits from combining constellations. GPS L5 and Galileo E5a share the same center frequency, and BeiDou B1C shares the GPS L1 / Galileo E1 center, so the combined GPS L1+L5 / Galileo E1+E5a dual-frequency receiver needs only two RF channels, and a single-frequency GPS+Galileo+BeiDou receiver needs one. The base station can be a physical reference station or a Virtual Reference Station (VRS) synthesized by the caster: the client reports the rover position to the caster via NMEA GGA sentences (enabled by default, see PVT.ntrip_send_gga below), as VRS and nearest-station services require.

For a dual-frequency receiver, the vector of unknown states to be estimated is defined as:

where \(\mathbf{B}_{i} = \left( B_{rb,i}^{(1)}, B_{rb,i}^{(2)}, ..., B_{rb,i}^{(m)} \right)^T\) are the single-difference carrier-phase biases (in cycles) between the rover \(r\) and the base station \(b\) for the \(i\)-th band. The measurement vector stacks double-differenced phase-range and pseudorange measurements:

where \(\boldsymbol{\Phi}_{i} = \left( \Phi_{rb,i}^{(12)}, \Phi_{rb,i}^{(13)}, ..., \Phi_{rb,i}^{(1m)}\right)^T\) and \(\mathbf{P}_{i} = \left( P_{rb,i}^{(12)}, P_{rb,i}^{(13)}, ..., P_{rb,i}^{(1m)} \right)^T\), with superscript \((1s)\) denoting the difference between the reference satellite and satellite \(s\). The equations that relate measurements and states are:

with partial derivatives matrix:

where \(\mathbf{D} = \left( \begin{array}{ccccc} 1 & -1 & 0 & \cdots & 0 \\ 1 & 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & \cdots & -1 \end{array} \right)\) is the single-differencing matrix and \(\mathbf{E} = \left( \mathbf{e}_{r}^{(1)}, \mathbf{e}_{r}^{(2)}, \mathbf{e}_{r}^{(3)}, ..., \mathbf{e}_{r}^{(m)} \right)^T\) is the matrix of receiver-to-satellite line-of-sight vectors. The state vector is propagated and updated with the same Extended Kalman Filter described in the Precise Point Positioning section above. When PVT.dynamics_model=1, the estimated velocity propagates the predicted position between epochs; when PVT.dynamics_model=2, the estimated acceleration also contributes to the prediction. In both cases, the process noise (configurable via PVT.sigma_acch and PVT.sigma_accv) grows with the time elapsed between epochs.

The reference satellite for double differencing is selected as the one with the lowest measurement variance (instead of the highest elevation), excluding satellites flagged with cycle slips. This selection rule is expected to behave better in urban conditions, where the received signal quality is a better quality proxy than elevation. Measurement noise follows the elevation-dependent error model described in the Single Point Positioning section, optionally extended with the SNR-dependent term (which in relative positioning uses the carrier-to-noise density ratios reported by both the rover and the base station) and the receiver-reported standard deviation term.

If an epoch provides fewer than four valid double-differenced carrier phases, the code-differenced solution is kept and reported with DGNSS quality, instead of being discarded.

Cycle slips and carrier-phase integrity

Undetected carrier-phase discontinuities corrupt the estimated ambiguities, so several complementary detectors are applied:

• Geometry-free combination: a cycle slip is declared when the geometry-free linear combination of carrier phases jumps between epochs by more than PVT.slip_threshold (it defaults to \(0.05\) m).
• Phase-Doppler difference: a detector compares the time-differenced carrier phase with the integrated Doppler, after removing the receiver clock error common to all satellites, estimated as the median range-rate residual over all of them. It is enabled by setting PVT.slip_threshold_doppler to a positive value, in m/s; it defaults to \(0\) (disabled).
• Carrier-phase integrity flags: the Tracking and Observables blocks flag carrier-phase discontinuities at their source: cycle slips after a signal reacquisition, and half-cycle jumps caused by a change in the telemetry-resolved phase polarity. The RTK engine resets or deweights the affected ambiguities instead of carrying them over, RINEX observation files report these events with standard loss-of-lock indicator (LLI) values, and the optional carrier-smoothing filter restarts instead of smoothing across the jump.

In the measurement update, innovations are screened against PVT.threshold_reject_innovation (code observables) and PVT.threshold_reject_innovation_phase (carrier-phase observables; setting it to \(5.0\) m in RTK modes is recommended). A carrier-phase bias that keeps producing outliers is reinitialized, instead of having its measurements rejected indefinitely.

Integer ambiguity resolution

Once the estimated states are obtained in the EKF measurement update, the float carrier-phase ambiguities can be resolved into integer values in order to improve accuracy and convergence time. The strategy is selected with the PVT.AR_GPS option: OFF, Continuous, Instantaneous, Fix-and-Hold, or PPP-AR.

At first, the estimated states and their covariance matrix are transformed to double-difference form by:

where \(\mathbf{G} = \left( \begin{array}{ccc} \mathbf{I}_{6 \times 6} & {} & {} \\ {} & \mathbf{D} & {} \\ {} & {} & \mathbf{D} \end{array} \right)\) is the single-difference to double-difference transformation matrix, built with an index-based formulation (in the style of RTKLIB 2.4.3) that keeps the bias bookkeeping consistent when several constellation groups are active. In this transformation, the single-difference carrier-phase biases are transferred to the double-difference form in order to eliminate receiver initial phase terms and obtain integer ambiguities \(\hat{\mathbf{N}}\) and their covariance \(\mathbf{Q}_N\). QZSS ambiguities are resolved in their own group instead of jointly with GPS, avoiding integer fixes across the GPS-QZSS inter-system bias. The most appropriate integer vector \(\breve{\mathbf{N}}\) is obtained by solving an ILS (integer least squares) problem expressed as:

To solve the ILS problem, the well-known efficient search strategy LAMBDA⁵ and its extension MLAMBDA⁶ are employed in the RTKLIB_PVT implementation. LAMBDA and MLAMBDA offer the combination of a linear transformation to shrink the integer vector search space and a skillful tree-search procedure in the transformed space.

The integer vector solution provided by these procedures is validated by the following simple Ratio-Test:

In this Ratio-Test, the ratio-factor \(R\), defined as the ratio of the weighted sum of the squared residuals by the second best solution \(\breve{\mathbf{N}}_2\) to the one by the best solution \(\breve{\mathbf{N}}\), is used to check the reliability of the solution. The validation threshold \(R_{thres}\) can be set with the PVT.min_ratio_to_fix_ambiguity option, and it defaults to \(3.0\). Alternatively, the threshold can be made dependent on the number of ambiguity pairs by setting PVT.ar_ratio_min and PVT.ar_ratio_max to different values: the effective threshold then scales between those bounds with the number of available ambiguities (equal values keep the fixed PVT.min_ratio_to_fix_ambiguity threshold).

Integer ambiguity resolution is driven by a management layer that improves robustness in non-ideal conditions:

• Ambiguity resolution is skipped while the float position variance is still above PVT.ar_max_position_variance (it defaults to \(0.25\) m^2; \(0\) disables this gate), avoiding false fixes while the filter converges.
• If PVT.ar_filter=true (the default), newly-risen satellites are excluded from ambiguity resolution, and the fix is retried when their inclusion degrades the AR ratio.
• When no fix is achieved with many satellites in view (at least PVT.min_drop_sats, defaulting to \(10\); \(0\) disables this mechanism), a single satellite at a time is cycled out of the ambiguity resolution and the fix is retried.
• Fixing and holding are gated on minimum satellite counts, configurable with PVT.min_fix_sats (it defaults to \(4\)) and PVT.min_hold_sats (it defaults to \(5\)).

After the validation, the ″FIXED″ solution of the rover antenna position and velocity \(\breve{\mathbf{r}}_r\) and \(\breve{\mathbf{v}}_r\) is obtained by solving the following equation:

If the validation fails, the ″FLOAT″ solution \(\hat{\mathbf{r}}_r\) and \(\hat{\mathbf{v}}_r\) is output instead.

Fix and Hold option

If PVT.AR_GPS is set to Fix-and-Hold, once the integer ambiguities are validated they are tightly constrained to their resolved values through pseudo-measurements, whose variance can be configured with PVT.var_holdamb (it defaults to \(0.1\) cycles^2). Holding requires at least PVT.min_hold_sats satellites providing validated ambiguities.

Base station corrections through NTRIP

The PVT block embeds an NTRIP (Networked Transport of RTCM via Internet Protocol) client that connects to an NTRIP caster, decodes RTCM 3 messages carrying the base station position (message types 1005 / 1006) and its observations — GPS L1 with L2 or L5 (legacy message type 1004 and MSM message types 1074-1077), Galileo E1 with E5a (MSM message types 1094-1097), and BeiDou B1C (MSM message types 1124-1127, preferring B1C over B1I in the shared first slot) — and feeds time-aligned reference data to the RTKLIB relative-positioning solver.

The client is enabled by setting PVT.ntrip_client_enabled=true, which requires PVT.positioning_mode to be set to Static or Kinematic and, per constellation and freely combined, GPS L1 C/A alone or together with one of L2C or L5, Galileo E1 alone or together with E5a, and BeiDou B1C; single-band sets run single-frequency RTK. Its main features are:

• NTRIP v2 with automatic v1 fallback: the client prefers NTRIP v2 and, after a fully-sent v2 exchange closes or times out before receiving response bytes, or returns HTTP 400, 501, or 505, it retries once on a fresh NTRIP v1 connection. Setting PVT.ntrip_version=1 forces the legacy protocol directly.
• TLS support: setting PVT.ntrip_tls_enabled=true enables TLS 1.2 or newer, with certificate validation against the system CA store and host name verification.
• Credential handling: HTTP Basic authentication is configured with PVT.ntrip_username and PVT.ntrip_password. Alternatively, the password can be read from an environment variable named in PVT.ntrip_password_env, keeping secrets out of the configuration file. Credentials are redacted from the RTKLIB trace files.
• Robust operation: the client reconnects automatically without blocking the GNU Radio flow graph, filters base station changes (a positive PVT.ntrip_station_id restricts the stream to that exact station ID), and drops stale corrections older than PVT.ntrip_max_correction_age_s (it defaults to \(5\) s).
• VRS support: the rover position is periodically reported upstream as an NMEA GGA sentence, as Virtual Reference Station and nearest-station mountpoints require (PVT.ntrip_send_gga, enabled by default; the cadence is set by PVT.ntrip_gga_period_ms, \(10\) s by default). No sentence is sent before the receiver produces its first position fix; the single-point bootstrap solution is enough for the caster to start serving the virtual station. Set PVT.ntrip_send_gga=false if the rover position must not be disclosed to the caster; physical-base mountpoints work either way.
• Explicit fallback: if corrections become unavailable and PVT.ntrip_fallback_to_single=true (the default), the receiver keeps operating with an explicitly labeled single-point solution.

The console reports the RTKLIB solution status: the First position fix and periodic Position at lines are tagged with [RTK FIXED], [RTK FLOAT], [DGNSS], [SBAS] or [PPP] (color-coded), and status transitions are announced once when they happen, including the LAMBDA ambiguity-resolution ratio and its threshold when an RTK fix is acquired or lost. Plain single-point operation keeps the classic, unmodified console output.

SBAS augmentation

The RTKLIB_PVT implementation can apply legacy SBAS L1 corrections, such as those broadcast by EGNOS, to a GPS L1 single-point solution. The receiver needs at least one S1 channel using the SBAS_L1_Telemetry_Decoder. CRC-valid SBAS frames are forwarded automatically from that decoder to the PVT block; the SBAS satellite itself is not used as a ranging source.

The correction controls are independent:

• PVT.satellite_ephemeris=SBAS applies fast and long-term satellite orbit/clock corrections. A GPS satellite without a current valid correction from the selected SBAS stream is excluded from the augmented solution.
• PVT.iono_model=SBAS applies the ionospheric grid delays and their associated quality information broadcast in SBAS message types 18 and 26.
• PVT.trop_model=SBAS applies the SBAS receiver-specification tropospheric model, commonly known as the MOPS model. It does not depend on a broadcast SBAS message.
• PVT.sbas_satellite selects the SBAS GEO correction stream when more than one is received.

This implementation provides a non-safety-critical SBAS Open Service solution. It uses the broadcast UDRE and GIVE information to reject unusable corrections and model their variance, but it does not compute protection levels or provide a Safety-of-Life solution.

Ionospheric Model

The ionosphere is a region of Earth’s upper atmosphere, from about 60 km to 1,000 km altitude, surrounding the planet with a shell of electrons and electrically charged atoms and molecules. This part of the atmosphere is ionized by ultraviolet, X-ray and shorter wavelengths of solar radiation, and this affects GNSS signals’ propagation speed.

The propagation speed of the GNSS electromagnetic signals through the ionosphere depends on its electron density, which is typically driven by two main processes: during the day, sun radiation causes ionization of neutral atoms producing free electrons and ions. During the night, the recombination process prevails, where free electrons are recombined with ions to produce neutral particles, which leads to a reduction in the electron density.

The frequency dependence of the ionospheric effect (in m) is described by the following expression:

where STEC is the Slant Total Electron Content, which describes the number of free electrons present within one square meter between the receiver and satellite \(s\). It is often reported in multiples of the so-called TEC unit, defined as \(\text{TECU} = 10^{16}\) el/m\(^2\). Ionospheric effects on the phase and code measurements have the opposite signs and have approximately the same amount. It causes a positive delay on code measurements (so it is included with a positive sign in the pseudorange measurement model) and a negative delay, or phase advance, in phase measurements (so it is included with a negative sign in the phase-range measurement model).

This dispersive nature (i.e., the ionospheric delay is proportional to the squared inverse of \(f_i\)) allows users to remove its effect up to more than 99.9% using two frequency measurements (as in the see ionosphere-free combination for dual-frequency receivers shown in the Precise Point Positioning algorithm described above), but single-frequency receivers have to apply an ionospheric prediction model to remove (as much as possible) this effect, that can reach up to several tens of meters.

Band selection

The PVT.iono_model option decides the pseudorange model applied to every satellite of a given system, regardless of how many bands each individual satellite is being tracked on:

• Iono-Free-LC forms the ionosphere-free linear combination of the first and second bands (GPS L1+L2 or L1+L5, Galileo E1+E5a, E1+E5b or E1+E6, BeiDou B1I+B3I, GLONASS L1+L2). A satellite whose second band is not available at a given epoch is excluded from the solution at that epoch, so that all satellites of the system share the same clock reference.

• OFF, Broadcast and SBAS use the first band alone, corrected with the broadcast group delay that matches the clock model of the ephemeris in use (TGD for GPS and BeiDou, \(BGD_{E1,E5a}\) or \(BGD_{E1,E5b}\) for Galileo depending on whether the F/NAV or the I/NAV clock is used), and the ionospheric delay is modeled or set to zero as selected. A second band present in the same observation record is ignored by the single point solution. When the first band is missing (for instance, a GPS L5-only or a Galileo E5a-only channel), the second band is used alone and the modeled ionospheric delay is scaled by \(\left(f_{1}/f_{2}\right)^2\).

BeiDou B2a observations (signal identifier 5D) are processed as single-frequency measurements: they are paired only with B-CNAV2 ephemerides (never with the D1/D2 or B-CNAV1 navigation data of the same satellite), and they are corrected with the \(TGD_{B2ap} + ISC_{B2ad}\) group delay broadcast in B-CNAV2. A receiver with only 5D channels computes a B2a-only single point solution; the combination of B2a with other BeiDou bands in the same receiver is not validated yet. The BeiDou B2a signal is only available in the next branch of the public repository and will be available in the next GNSS-SDR stable release.

This rule keeps all satellites of a system on a single, consistent model. Mixing per-satellite single-band and dual-band pseudoranges within one solution would introduce two different clock references, and would also fold the receiver’s inter-band delay into the position. That delay is not calibrated by GNSS-SDR: in particular, two RF channels processed with input filters of different lengths differ by their group-delay difference (for instance, 29 versus 289 taps at 60 Msps amounts to about 650 m in the code measurements), so multi-band configurations should use input filters of the same length in every RF channel. Dual-frequency users who want the ionosphere-free combination in the single point solution must select PVT.iono_model=Iono-Free-LC explicitly.

Broadcast

For ionosphere correction for single-frequency GNSS users, GPS navigation data include the following broadcast ionospheric parameters:

By using these ionospheric parameters, the L1 ionospheric delay \(I_{r,1}^{(s)}\) (in m) can be derived by the following procedure⁷ (this model is often called as the Klobuchar model⁸):

This correction is activated when PVT.iono_model is set to Broadcast.

SBAS

If PVT.iono_model is set to SBAS, the ionospheric delay is obtained from the SBAS ionospheric grid. Message type 18 defines the ionospheric grid point masks, and message type 26 provides the vertical delays and GIVE quality indicators. The correction is applied only where the received grid provides valid coverage.

Tropospheric Model

The troposphere is the lowest portion of Earth’s atmosphere, and contains 99% of the total mass of water vapor. The average depths of the troposphere are 20 km in the tropics, 17 km in the mid-latitudes, and 7 km in the polar regions in winter. The chemical composition of the troposphere is essentially uniform, with the notable exception of water vapor, which can vary widely. The effect of the troposphere on the GNSS signals appears as an extra delay in the measurement of the signal traveling time from the satellite to the receiver. This delay depends on the temperature, pressure, humidity as well as the transmitter and receiver antennas location, and it is related to air refractivity, which in turn can be divided into hydrostatic, i.e., dry gases (mainly \(N_2\) and \(O_2\)), and wet, i.e., water vapor, components:

• Hydrostatic component delay: Its effect varies with local temperature and atmospheric pressure in quite a predictable manner, besides its variation is less than the 1% in a few hours. The error caused by this component is about \(2.3\) meters in the zenith direction and \(10\) meters for lower elevations (\(10^{o}\) approximately).

• Wet component delay: It is caused by the water vapor and condensed water in form of clouds and, thence, it depends on weather conditions. The excess delay is small in this case, only some tens of centimetres, but this component varies faster than the hydrostatic component and in a quite random way, being very difficult to model.

The troposphere is a non-dispersive media with respect to electromagnetic waves up to 15 GHz, so the tropospheric effects are not frequency-dependent for the GNSS signals. Thence, the carrier phase and code measurements are affected by the same delay, and this effect can not be removed by combinations of dual-frequency measurements.

Saastamoinen

The standard atmosphere can be expressed as:⁹

where \(p\) is the total pressure (in hPa), \(T\) is the absolute temperature (in K) of the air, \(h\) is the geodetic height above MSL (mean sea level), \(e\) is the partial pressure (in hPa) of water vapor and \(h_{rel}\) is the relative humidity. The tropospheric delay \(T_{r}^{(s)}\) (in m) is expressed by the Saastamoinen model with \(p\), \(T\) and \(e\) derived from the standard atmosphere:

where \(z^{(s)}\) is the zenith angle (rad) as \(z^{(s)} = \frac{\pi}{2} - El_{r}^{(s)}\), where \(El_{r}^{(s)}\) is elevation angle of satellite direction (rad).

The standard atmosphere and the Saastamoinen model are applied in the case that the processing option PVT.trop_model is set to Saastamoinen, where the geodetic height is approximated by the ellipsoidal height and the relative humidity is fixed to 70%.

SBAS

If PVT.trop_model is set to SBAS, the tropospheric model defined in the SBAS receiver specifications is applied. This is commonly known as the MOPS model. Refer to Appendix A.4.2.4 of the MOPS reference¹⁰ for details.

Estimate the tropospheric zenith total delay

If the processing option PVT.trop_model is set to Estimate_ZTD, a more precise troposphere model is applied with strict mapping functions as:

where \(Z_{T,t}\) is the tropospheric zenith total delay (in meters), \(Z_{H,r}\) is the tropospheric zenith hydro‐static delay (in meters), \(m_{H}\left(El_{r}^{(s)}\right)\) is the hydro‐static mapping function and \(m_{W}\left(El_{r}^{(s)}\right)\) is the wet mapping function. The tropospheric zenith hydro‐static delay is given by Saastamoinen model described above with the zenith angle \(z = 0\) and relative humidity \(h_{rel} = 0\). For the mapping function, the software employs the Niell mapping function¹¹. The zenith total delay \(Z_{T,r}\) is estimated as an unknown parameter in the parameter estimation process.

Estimate the tropospheric zenith total delay and gradient

If the processing option trop_model is set to Estimate_ZTD_Grad, a more precise troposphere model is applied with strict mapping functions as¹²:

where \(Az_{r}^{(s)}\) is the azimuth angle of satellite direction (rad), and \(G_{E,r}\) and \(G_{N,r}\) are the east and north components of the tropospheric gradient, respectively. The zenith total delay \(Z_{T,r}\) and the gradient parameters \(G_{E,r}\) and \(G_{N,r}\) are estimated as unknown parameters in the parameter estimation process.

A de-noising Kalman filter for the PVT solution

The PVT block can apply a simple Kalman filter to the computed PVT solutions. This filter can be enabled by setting PVT.enable_pvt_kf=true in the configuration file. The structure of this filter is as follows:

• State model: \(\begin{equation} \mathbf{x} = \left[ x, y, z, v_x, v_y, v_z \right]^{T} \end{equation}\)

  \[\begin{equation} \mathbf{x}_k = \mathbf{F} \mathbf{x}_{k-1} + \mathbf{v}_k~, \quad \mathbf{v}_k \sim \mathcal{N}(\mathbf{0},\mathbf{Q}) \end{equation}\] \[\begin{equation} \textbf{F} = \left[ \begin{array}{cccccc} 1 & 0 & 0 & T & 0 & 0 \\ 0 & 1 & 0 & 0 & T & 0 \\ 0 & 0 & 1 & 0 & 0 & T \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right] \end{equation}\] \[\begin{equation} \textbf{Q} = \begin{bmatrix} \sigma_{s\_pos}^{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & \sigma_{s\_pos}^{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & \sigma_{s\_pos}^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{s\_vel}^{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \sigma_{s\_vel}^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \sigma_{s\_vel}^{2} \end{bmatrix} \end{equation}\]

• Measurement model: \(\begin{equation} \mathbf{z} = \left[ x , y , z , v_{x}, v_{y}, v_{z} \right]^{T} \end{equation}\)

  \[\begin{equation} \mathbf{z}_k = \mathbf{H}\mathbf{x}_k + \mathbf{w}_k , \quad \mathbf{w}_k \sim \mathcal{N}(\mathbf{0},\mathbf{R}) \end{equation}\] \[\begin{equation} \textbf{H} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \end{equation}\] \[\begin{equation} \textbf{R} = \begin{bmatrix} \sigma_{m\_pos}^{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & \sigma_{m\_pos}^{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & \sigma_{m\_pos}^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{m\_vel}^{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \sigma_{m\_vel}^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \sigma_{m\_vel}^{2} \end{bmatrix} \end{equation}\]

• Initialization: \(\begin{equation} \mathbf{x}_{0|0} = \left[ \begin{array}{cccc} x_{0} & y_{0} & z_{0} & v_{x_{0}} & v_{y_{0}} & v_{z_{0}} \end{array} \right]^T \end{equation}\)

  \[\begin{equation} \mathbf{P}_{0|0} = \begin{bmatrix} \sigma_{s\_pos}^{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & \sigma_{s\_pos}^{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & \sigma_{s\_pos}^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{s\_vel}^{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \sigma_{s\_vel}^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \sigma_{s\_vel}^{2} \end{bmatrix} \end{equation}\]

• Prediction: \(\begin{equation} \hat{\mathbf{x}}_{k|k-1} = \mathbf{F} \hat{\mathbf{x}}_{k-1|k-1} \end{equation}\)

  \[\begin{equation} \mathbf{P}_{k|k-1} = \mathbf{F} \mathbf{P}_{k-1|k-1} \mathbf{F}^T + \mathbf{Q} \end{equation}\]

• Update: \(\begin{equation} \mathbf{K}_k = \mathbf{P}_{k|k-1} \mathbf{H}^T \left( \mathbf{H}\mathbf{P}_{k|k-1} \mathbf{H}^T + \mathbf{R} \right)^{-1} \end{equation}\)

  \[\begin{equation} \hat{\mathbf{x}}_{k|k} = \hat{\mathbf{x}}_{k|k-1} + \mathbf{K}_k \left( \mathbf{z}_k - \mathbf{H}_k\hat{\mathbf{x}}_{k|k-1} \right) \end{equation}\] \[\begin{equation} \mathbf{P}_{k|k} = \left( \mathbf{I} - \mathbf{K}_{k} \mathbf{H} \right)\mathbf{P}_{k|k-1} \end{equation}\]

The following parameters are exposed in the configuration, here with their default values:

• \[\sigma_{m\_pos} = \text{PVT.kf_measures_ecef_pos_sd_m} = 1.0 \text {, in [m].}\]
• \[\sigma_{m\_vel} = \text{PVT.kf_measures_ecef_vel_sd_ms} = 0.1 \text {, in [m/s].}\]
• \[\sigma_{s\_pos} = \text{PVT.kf_system_ecef_pos_sd_m} = 0.01 \text {, in [m].}\]
• \[\sigma_{s\_vel} = \text{PVT.kf_system_ecef_vel_sd_ms} = 0.001 \text {, in [m/s].}\]

Output formats

Depending on the specific application or service that is exploiting the information provided by GNSS-SDR, different internal data will be required. The software provides such output data in standard formats:

KML, GeoJSON, GPX

For Geographic Information Systems, map representation and Earth browsers: KML, GeoJSON, and GPX files are generated by default, upon the computation of the first position fix.

RINEX

For post-processing applications: RINEX 2.11, 3.02, or 4.02. Version 3.02 is generated by default, and versions 2.11 or 4.02 can be requested by setting PVT.rinex_version=2 or PVT.rinex_version=4 in the configuration file. NOTE: Version 4 is only available in the next branch of the public repository and will be available in the next GNSS-SDR stable release.

BeiDou B2a observations are reported with the observation code 5D (data component). Navigation records for the B-CNAV2 message are only written in RINEX version 4 (CNV2 records, including \(ISC_{B2ad}\)); since RINEX 3 has no representation for B-CNAV2 data, those navigation records are omitted in version 3 files. The BeiDou B2a signal is only available in the next branch of the public repository and will be available in the next GNSS-SDR stable release.

IMPORTANT: In order to get well-formatted GeoJSON, KML, GPX, and RINEX files, always terminate gnss-sdr execution by pressing key ‘q’ and then key ‘ENTER’. Those files will be automatically deleted if no position fix has been obtained during the execution of the software receiver.

NMEA-0183

For sensor integration: NMEA-0183. A text file containing NMEA messages is stored with a default name of gnss_sdr_pvt.nmea, configurable via PVT.nmea_dump_filename. In addition, NMEA messages can be forwarded to a serial port by setting PVT.flag_nmea_tty_port=true. The default port is /dev/tty1, and can be configured via PVT.nmea_dump_devname.

RTCM-104

For real-time, possibly networked processing: RTCM-104 messages, v3.2. A TCP/IP server of RTCM messages can be enabled by setting PVT.flag_rtcm_server=true in the configuration file, and will be active during the execution of the software receiver. By default, the server will operate on port 2101 (which is the recommended port for RTCM services according to the Internet Assigned Numbers Authority, IANA), and will identify the Reference Station with ID=1234. These values can be changed with PVT.rtcm_tcp_port and PVT.rtcm_station_id. The rate of the generated RTCM messages can be tuned with the options PVT.rtcm_MT1045_rate_ms (it defaults to 5000 ms), PVT.rtcm_MT1019_rate_ms (it defaults to 5000 ms), PVT.rtcm_MSM_rate_ms (it defaults to 1000 ms). The RTCM messages can also be forwarded to the serial port PVT.rtcm_dump_devname (it defaults to /dev/pts/1) by setting PVT.flag_rtcm_tty_port=true in the configuration file.

Custom streaming

In addition to the standard output formats, the PVT block offers a custom mechanism for streaming its internal data members to local or remote clients over UDP through a monitoring port which can be enabled by setting PVT.enable_monitor=true in the configuration file. This feature is very useful for real-time monitoring of the PVT block and its outputs. By default, the data is streamed to the localhost address on port 1234 UDP. These settings can be changed with PVT.monitor_client_addresses and PVT.monitor_udp_port. The streamed data members are serialized via Protocol Buffers into a format defined at monitor_pvt.proto. This allows other applications to easily read those messages, either using C++, Java, Python, C#, Dart, Go, or Ruby, among other languages, hence enhancing Interoperability.

The following table shows the complete list of streamed parameters:

Each TrackedSatellite entry contains the following fields:

Signals are listed individually (one entry per satellite and signal), not merged: a satellite whose signals were combined appears as one entry per signal, all flagged with combined = true. The azimuth and elevation are reported as computed by the solver, so a corrupt ephemeris or almanac can result in NaN values for those fields; client applications are expected to handle that case explicitly (for instance, by not drawing that satellite in a sky plot). Such a satellite is never used in the position solution.

The PVT monitor can also stream GPS and Galileo ephemeris data by setting PVT.enable_monitor_ephemeris=true in the configuration file. The streamed data members are serialized via Protocol Buffers into formats defined at gps_ephemeris.proto and galileo_ephemeris.proto, prepended by character G for GPS data and by character E for Galileo data. By default, data are streamed to the localhost address on port 1234 UDP. These settings can be changed with PVT.monitor_ephemeris_client_addresses and PVT.monitor_ephemeris_udp_port parameters in the configuration file.

Read more about standard output formats on our Interoperability page.

Implementation: RTKLIB_PVT

This implementation makes use of the positioning libraries of RTKLIB, a well-known open-source program package for standard and precise positioning. It accepts the following parameters:

PVT implementation: RTKLIB_PVT.

Example:

;######### PVT CONFIG ############
PVT.implementation=RTKLIB_PVT
PVT.positioning_mode=PPP_Static
PVT.output_rate_ms=100
PVT.display_rate_ms=500
PVT.iono_model=Broadcast
PVT.trop_model=Saastamoinen
PVT.flag_rtcm_server=true
PVT.flag_rtcm_tty_port=false
PVT.rtcm_dump_devname=/dev/pts/1
PVT.rtcm_tcp_port=2101
PVT.rtcm_MT1019_rate_ms=5000
PVT.rtcm_MT1045_rate_ms=5000
PVT.rtcm_MT1097_rate_ms=1000
PVT.rtcm_MT1077_rate_ms=1000
PVT.rinex_version=2

For a GPS L1 single-point solution augmented with SBAS corrections, use an S1 telemetry channel and configure PVT as follows:

;######### SBAS L1 TELEMETRY DECODER CONFIG ############
TelemetryDecoder_S1.implementation=SBAS_L1_Telemetry_Decoder

;######### PVT CONFIG WITH SBAS CORRECTIONS ############
PVT.implementation=RTKLIB_PVT
PVT.positioning_mode=Single
PVT.satellite_ephemeris=SBAS
PVT.sbas_satellite=0
PVT.iono_model=SBAS
PVT.trop_model=SBAS

The receiver must also define at least one SBAS L1 channel, for example with Channels_S1.count=1. Set PVT.sbas_satellite to a specific GEO PRN when the receiver tracks multiple SBAS signals and a particular correction stream is required.

For an RTK solution with corrections received from an NTRIP caster, configure the receiver with a supported channel set — for instance, GPS L1 C/A + L2C with Channels_1C.count=8 and Channels_2S.count=8, a combined GPS L1+L5 / Galileo E1+E5a receiver with Channels_1C, Channels_L5, Channels_1B, and Channels_5X channels, or a single-frequency GPS+Galileo receiver with only Channels_1C and Channels_1B — and set up PVT as follows:

;######### PVT CONFIG WITH RTK VIA NTRIP ############
PVT.implementation=RTKLIB_PVT
PVT.positioning_mode=Kinematic
PVT.AR_GPS=Fix-and-Hold
PVT.threshold_reject_innovation_phase=5.0
PVT.ntrip_client_enabled=true
PVT.ntrip_caster_address=caster.example.org
PVT.ntrip_caster_port=2101
PVT.ntrip_mountpoint=MOUNTPOINT
PVT.ntrip_username=user
PVT.ntrip_password_env=NTRIP_PASSWORD
PVT.ntrip_tls_enabled=false

In this example, the caster password is read from the NTRIP_PASSWORD environment variable, so it does not need to be written in the configuration file. If the mountpoint is a Virtual Reference Station or a nearest-station service, no additional settings are needed: the client reports the rover position to the caster via NMEA GGA sentences by default (see PVT.ntrip_send_gga). The console will tag position fixes with [RTK FIXED], [RTK FLOAT], or [DGNSS] labels, and will announce solution status transitions, including the LAMBDA ambiguity-resolution ratio when an RTK fix is acquired or lost. This feature is only available in the next branch of the public repository and will be available in the next GNSS-SDR stable release.

The generation of output files is controlled by the parameter output_enabled. If set to true (which is its default value), RINEX, XML, GPX, KML, GeoJSON, NMEA and binary RTCM files will be generated. You can turn off the generation of such files by setting output_enabled=false, and then select, for instance, rinex_output_enabled=true or kml_output_enabled=true. Files are stored in the path indicated in output_path, which by default is the current folder (that is, the folder from which GNSS-SDR was called). This can be changed for all outputs (for instance, output_path=gnss-products or output_path=/home/user/Documents/gnss-products/day1), or it can be defined per type of output (e.g., rinex_output_path=gnss-products/rinex, gpx_output_path=gnss-products/gpx, geojson_output_path=gnss-products/geojson, etc.).

Example:

PVT.output_enabled=false
PVT.rtcm_output_file_enabled=false
PVT.gpx_output_enabled=true
PVT.geojson_output_enabled=true
PVT.kml_output_enabled=true
PVT.xml_output_enabled=true
PVT.rinex_output_enabled=true
PVT.nmea_output_file_enabled=false
PVT.output_path=gnss-products/others
PVT.gpx_output_path=gnss-products/gpx
PVT.kml_output_path=./
PVT.xml_output_path=./
PVT.rinex_output_path=gnss-products/rinex

This will create in your current directory:

.
├── PVT_181028_093651.kml
├── gnss-products
│   ├── gpx
│   │   └── PVT_181028_093651.gpx
│   ├── others
│   │   └── PVT_181028_093651.geojson
│   └── rinex
│       ├── GSDR301j36.18N
│       └── GSDR301j36.18O
└── gps_ephemeris.xml

In order to shut down the generation of output files, you can just include in your configuration file the line:

PVT.output_enabled=false

Please note that this only concerns the generation of mentioned file formats, and it does not affect the generation of dump files activated in the configuration of each processing block. If the RTCM server is activated with flag_rtcm_server=true, it will still work even if the binary RTCM file is deactivated with rtcm_output_file_enabled=false.

References